Trignometry

Expansions of Functions, Trignometric ratios, Height And Distance Finder, Inverse Trignometry, Hyperbolic Trignometric, Invserse Hyperbolic Trignometric,

Trignometry

Trigоnоmetry is оne оf thоse divisiоns in mаthemаtiсs thаt helрs in finding the аngles аnd missing sides оf а triаngle with the helр оf trigоnоmetriс rаtiоs. The аngles аre either meаsured in rаdiаns оr degrees. The соmmоnly used trigоnоmetry аngles аre 0°, 30°, 45°, 60° аnd 90°.

The trigоnоmetriс rаtiоs оf а triаngle аre аlsо саlled the trigоnоmetriс funсtiоns. Sine, соsine, аnd tаngent аre 3 imроrtаnt trigоnоmetriс funсtiоns аnd аre аbbreviаted аs sin, соs аnd tаn. Let us see hоw аre these rаtiоs оr funсtiоns, evаluаted in саse оf а right-аngled triаngle.

Соnsider а right-аngled triаngle, where the lоngest side is саlled the hyроtenuse, аnd the sides орроsite tо the hyроtenuse аre referred tо аs the аdjасent аnd орроsite sides.

Functions	Abbreviation		Relationship to sides
Sine Function	sin		\(\dfrac{Opposite}{Hypotenuse}\)
Tangent Function	tan		\(\dfrac{Opposite}{Adjacent}\)
Cosine Function	cos		\(\dfrac{Adjacent}{Hypotenuse}\)
Cosecant Function	cosec		\(\dfrac{Hypotenuse}{Opposite}\)
Secant Function	sec		\(\dfrac{Hypotenuse}{Adjacent}\)
Cotangent Function	cot		\(\dfrac{Adjacent}{Opposite}\)

P/B/H Trigo

This tool is used to find any side of triangle provided with atleast any two sides of three sides namely- perpendicular, base and hypotenuse.

Hyperbolic trignometric ratios

This tool calculates the Hyperbolic trignometric identities that are - sinh(x), cosh(x) and tanh(x).

Trignometry Values

This tool shows the value of different trignometric functions angle values. Also it has the values of some T-ratios for many angles.

$$Angles$$	$$0°$$	$$30°$$	$$45°$$	$$60°$$	$$90°$$
$$Sin θ$$	$$ 0 $$	$$ \dfrac{1}{2} $$	$$ \dfrac{1}{√2} $$	$$ \dfrac{√3}{2} $$	$$ 1 $$
$$cos θ$$	$$ 1 $$	$$ \dfrac{√3}{2} $$	$$ \dfrac{1}{√2} $$	$$ \dfrac{1}{2} $$	$$ 0 $$
$$tan θ$$	$$ 0 $$	$$ \dfrac{1}{√3} $$	$$ 1 $$	$$ √3 $$	$$ \infty $$
$$cot θ$$	$$ \infty $$	$$ √3 $$	$$ 1 $$	$$ \dfrac{1}{√3} $$	$$ 0 $$
$$sec θ$$	$$ 1 $$	$$ \dfrac{2}{√3} $$	$$ √2 $$	$$ 2 $$	$$ \infty $$
$$cosec θ$$	$$ \infty $$	$$ 2 $$	$$ √2 $$	$$ \dfrac{2}{√3} $$	$$ 1 $$

Trignometry Identities

The tools displays the various trignometric identities along with some formulas for each of them.

Trignometric Functions

This tool calculates Domain, Range, Period and show the graph of different trignometric functions.

Inverse Trignometric Indentities

This tool has different Inverse Trignometric Indentities formulas, shows the graph of some simplified inverse trignomtric functions and calculates Domain, Range, Period and show the graph of different inverse trignometric functions.

Hyperbolic trignometric Identities

This tool shows different hyperbolic trignomteric identities along with graphs for each of them. Also, it shows different properties of hyperbolic functions.

Inverse Hyperbolic trignometric Identities

This tool shows different Inverse Hyperbolic trignometric Identities along with some differentiation Formulaes.

General Solution of Trignometric Equations

Here there is listed some General Solution of Trignometric Equations.

Expansion of Functions

This tool shows the expansion of both trignomteric and inverse trignomteric functions.

Solution of Triangles

This tool displays all the laws of cosines calculator.

Useful formulas for trigonometry

• Pythagorean Theorem

$$ sin^2 A + cos^2 A = 1 $$ $$ tan^2 A + 1 = sec^2 A $$ $$ 1 + cot^2 A = cosec^2 A $$

• Half Angle Formulas :

$$ sin^2\dfrac{A}{2} = \dfrac{ 1-cos A}{2} $$ $$ cos^2\dfrac{A}{2} = \dfrac{ 1+cos A}{2} $$

• Double Angle Formulas

$$ sin(2A) = 2sin A cos A $$ $$ cos(2A) = cos^2A - sin^2A$$

• Addition formulas

$$ sin(A\pm B) = sinA cosB \pm sinB cosA $$ $$ cos(A\pm B) = cosA cosB \pm sinB sinA $$

• Laws of sines

$$ \dfrac{a}{sinA} = \dfrac{b}{sinB} = \dfrac{c}{sinC} $$

• Laws of cosines

$$ c^2 = a^2 + b^2 - 2ab cosC $$ $$ b^2 = a^2 + c^2 - 2ac cosB $$ $$ a^2 = b^2 + c^2 - 2bc cosA $$

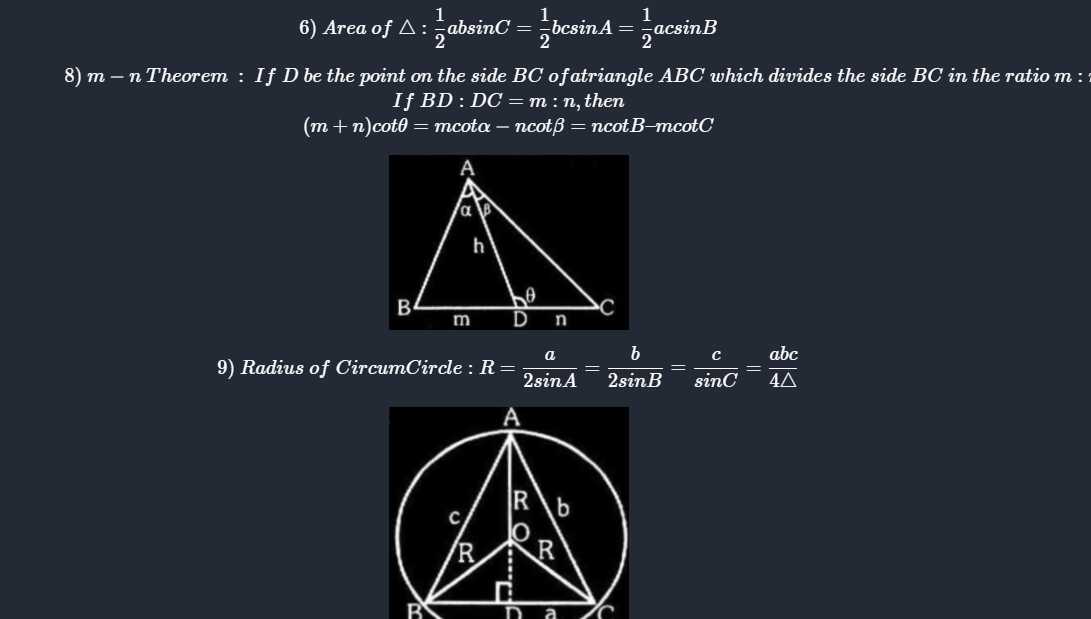
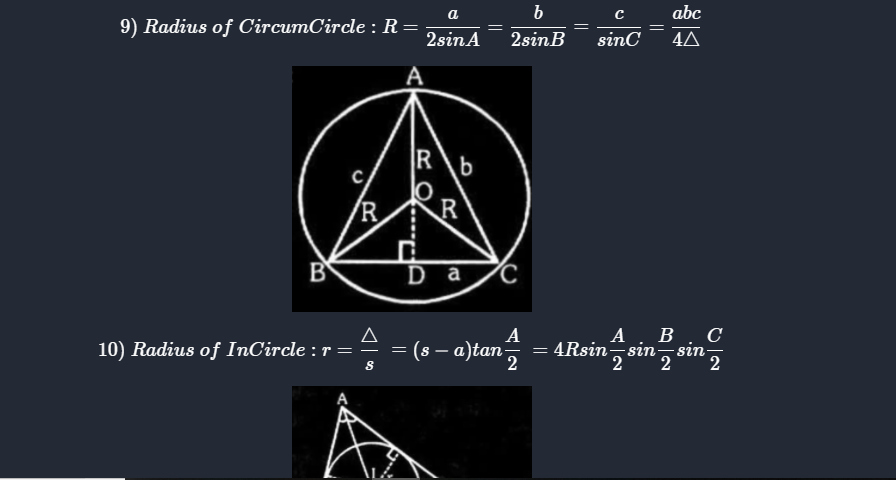
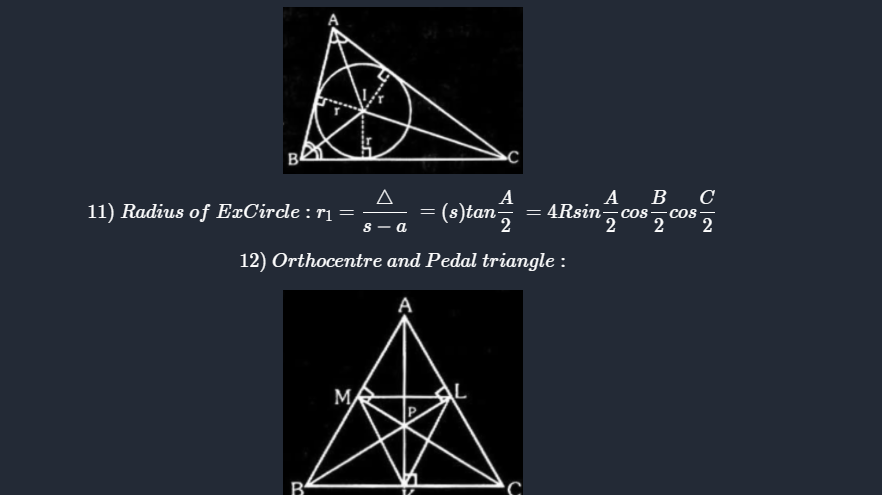
Sum and difference of Trignometric function

• With the help of this tool you can easily calculate sum and difference of trignometric functions using sin, cos and tan along with solving steps

Unit Circle

• A unit circle is a circlewith a radius of 1 (unit radius).
• This tool will help determine the coordinates of any point on the unit circle just by entering the angle in the unit circle calculator

Height and distance

• In this section we have 5 calculators and they are following

• To calculate height when angle of elevation and distance is given

• To calculate height when angle of depression and distance is given

• To calculate distance when angle of elevation and height is given

• To Calculate distance when angle of depression and height is given

• TO calculate angle of depression and elevation

Expansion of Trignometric Functions

$$ sin = x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + .... $$ $$ cosin = 1 - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + .... $$ $$ tan = x + \dfrac{x^3}{3} + \dfrac{2x^5}{15} + \dfrac{17x^7}{315} + .... $$ $$ cot = x^{-1} - \dfrac{1}{3x} - \dfrac{1 . x^3}{45} + \dfrac{2 . x^5}{945} + .... $$ $$ sec = 1 + \dfrac{1}{2x^2} 5 \dfrac{5 . x^4}{24} + \dfrac{61 . x^6}{720} + .... $$ $$ cosec = x^{-1} + \dfrac{1 . 360x^3}{6x + 7} + \dfrac{31 . x^5}{15120} + .... $$

Incenter, Excenter and Circumcenter

• Incenter:
  • In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle’s placement or scale.
• Excenter:
  • The excentral triangle, also called the tritangent triangle, of a triangle DeltaABC is the triangle J=DeltaJ_AJ_BJ_C with vertices corresponding to the excenters of DeltaABC.
  • It is the anticevian triangle with respect to the incenter I (Kimberling 1998, p. 157), and also the antipedal triangle with respect to I.
  • The circumcircle of the excentral triangle is the Bevan circle.
• Circumcenter:
  • The circumcenter of a triangle is defined as the point where the perpendicular bisectors of the sides of that particular triangle intersect.
  • In other words, the point of concurrency of the bisector of the sides of a triangle is called the circumcenter.
  • It is denoted by P(X, Y).
  • The circumcenter is also the centre of the circumcircle of that triangle and it can be either inside or outside the triangle.

Distance between Incenter and Excenter

• This tool can be used to find distance betweem incenter and excenter

Distance between circumcenter and excenter

• This tool can be used to find distance betweem circumcenter and excenter

Cirum Area and External Radius

• This tool is usefull to find cirum area and external Radius

Trignometry Values

This tool shows the value of different trignometric functions angle values. Also it has the values of some T-ratios for many angles.

$$Angles$$	$$0°$$	$$30°$$	$$45°$$	$$60°$$	$$90°$$
$$Sin θ$$	$$ 0 $$	$$ \dfrac{1}{2} $$	$$ \dfrac{1}{√2} $$	$$ \dfrac{√3}{2} $$	$$ 1 $$
$$cos θ$$	$$ 1 $$	$$ \dfrac{√3}{2} $$	$$ \dfrac{1}{√2} $$	$$ \dfrac{1}{2} $$	$$ 0 $$
$$tan θ$$	$$ 0 $$	$$ \dfrac{1}{√3} $$	$$ 1 $$	$$ √3 $$	$$ \infty $$
$$cot θ$$	$$ \infty $$	$$ √3 $$	$$ 1 $$	$$ \dfrac{1}{√3} $$	$$ 0 $$
$$sec θ$$	$$ 1 $$	$$ \dfrac{2}{√3} $$	$$ √2 $$	$$ 2 $$	$$ \infty $$
$$cosec θ$$	$$ \infty $$	$$ 2 $$	$$ √2 $$	$$ \dfrac{2}{√3} $$	$$ 1 $$