Linear Algebra

Matrices, mathematical Modeling, Euclid geometry, Sets, Realtions And Functions, Sigma, Cramers Rule, Cayley Hamilton Theorem, Arithmetic Progression, Geometric Progression, Harmonic Progression, Golden and Silver Ratio

Matrices

What is a Matrix?

A matrix is a rectangular array of elements, usually numbers,In general, an matrix looks like:

$$ \begin{equation} A_{m,n} = \begin{bmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m,2} & \cdots & a_{m,n} \end{bmatrix} \end{equation} $$

matrix is enclosed by [ ] or ( ) or | | | | Compact form the above matrix is represented by [aij]m x n or A = [aij]

• Element of a Matrix The numbers a11, a12 … etc., in the above matrix are known as the element of the matrix, generally represented as aij , which denotes element in ith row and jth column.
• Order of a Matrix In above matrix has m rows and n columns, then A is of order m x n.

Why use Matrices?

With Matrix we can represent data, we can use matrices to work on multiple linear equations and mathematical equations, In many time-sensitive engineering applications, we can add, subtract or even multipy to get good approximations of much more complicated calculations. We use matrices in mathematics because often we need to deal with several variables at once—eg the coordinates of a point in the plane are written (x, y) or in space as (x, y, z) and these are often written as column matrices in the following form:

$$ \begin{equation} \begin{pmatrix} x \\ y \end{pmatrix} and \begin{pmatrix} x \\ y \\ z \end{pmatrix} \end{equation} $$

Types of matrix

• Column Matrix: A Matrix with one column, where order is Mx1

$$ \begin{equation}eg: \begin{bmatrix} 0 \\ -6 \\ 4 \end{bmatrix} _{m,1} \end{equation} $$

• Row Matrix: A Matrix with one row, where order is 1xN

$$ \begin{equation}eg: \begin{bmatrix} 0 & 19 &-2 \end{bmatrix} _{1,n} \end{equation} $$

• Square Matrix: A Matrix with equal row and column, where order is NxN

$$ \begin{equation}eg: \begin{bmatrix} 0 & 19 & -2 \\ 5 & -1 & 12 \\ 4 & 8 & 0 \end{bmatrix} _{n,n} \end{equation} $$

• Diagonal Matrix: A square matrix whose all the elements except the diagonal elements are zeroes, is called a diagonal matrix where if aij = 0, when i ≠ j.

$$ \begin{equation}eg: \begin{bmatrix} 3 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 5 \end{bmatrix} _{m,m} \end{equation} $$

• Scalar Matrix: A diagonal matrix whose all diagonal elements are same (non-zero), is called a scalar matrix.

Note: A scalar matrix is a diagonal matrix but a diagonal matrix may or may not be a scalar matrix

$$ \begin{equation}eg: \begin{bmatrix} 3 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{bmatrix} _{m,m} \end{equation} $$

• Unit or Identity Matrix: A diagonal matrix in which all diagonal elements are ‘1’ and all non-diagonal elements are zero, is called an identity matrix. It is denoted by I, where aij = 1, when i = j and aij = 0, when i ≠ j.

$$ \begin{equation}I = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} _{m,m} \end{equation} $$

• Zero or Null Matrix: A matrix is said to be a zero or null matrix, if its all elements are 0

$$ \begin{equation}Eg \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} _{m,m} \end{equation} $$

• Equality of Matrices: Two matrices A and B are said to be equal, if
  • order of A and B are same.
  • corresponding elements of A and B are same i.e. aij = bij, ∀ i and j.

$$ \begin{equation}eg: \begin{bmatrix} 1 & 2 \\ 0 & 3 \end{bmatrix} and \begin{bmatrix} 1 & 2 \\ 0 & 3 \end{bmatrix} are \enspace equal \enspace ,but \begin{bmatrix} 1 & 2 \\ 0 & 3 \end{bmatrix} and \begin{bmatrix} 1 & 7 \\ 4 & 3 \end{bmatrix} are \enspace not \enspace equal \end{equation} $$

Opeartions on a single matrix

• Transpose of a matrix
  • The transpose of a matrix is a new matrix whose rows are the columns of the original matrix. Below is a matrix and its transpose:
  • The superscript “T” means “transpose”.

$$ \begin{equation}A = \begin{bmatrix} 5 & 4 & 3 \\ 4 & 0 & 4 \\ 7 & 10 & 3 \end{bmatrix}^T \enspace = \begin{bmatrix} 5 & 4 & 7 \\ 4 & 0 & 10 \\ 3 & 4 & 3 \end{bmatrix} \end{equation} $$

• Determinant of a matrix
• The determinant of a matrix is a special number that can be calculated from a square matrix which helps us find the inverse of a matrix, tells us things about the matrix that are useful in systems of linear equations, calculus and many more.
• To calculate the determinant first of all the matrix must be square (i.e. have the same number of rows as columns). Then it is just basic arithmetic.
• The symbol for determinant is two vertical lines either side:

• Formula to caluclate determinant is :

  A

  = a(ei − fh) − b(di − fg) + c(dh − eg)

$$ \begin{equation}A = \begin{vmatrix} a & b & c \\ d & e & f \\ g & g & i \end{vmatrix} \end{equation} $$

$$ \begin{equation} \begin{vmatrix} A \\ \end{vmatrix} = \enspace a \begin{vmatrix} e & f \\ h & i \\ \end{vmatrix} - \enspace b \begin{vmatrix} d & f \\ g & i \\ \end{vmatrix} + \enspace c \begin{vmatrix} d & e \\ g & h \\ \end{vmatrix} \end{equation} $$

$$ \begin{equation}Example = \begin{vmatrix} 6 & 1 & 1 \\ 4 & -2 & 5 \\ 2 & 8 & 7 \\ \end{vmatrix} \end{equation} $$

$$ |A| = 6×(−2×7 − 5×8) − 1×(4×7 − 5×2) + 1×(4×8 − (−2×2)) $$ $$ 6×(−54) − 1×(18) + 1×(36) $$ $$ −306 $$

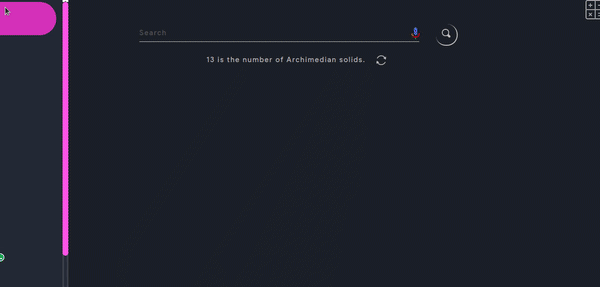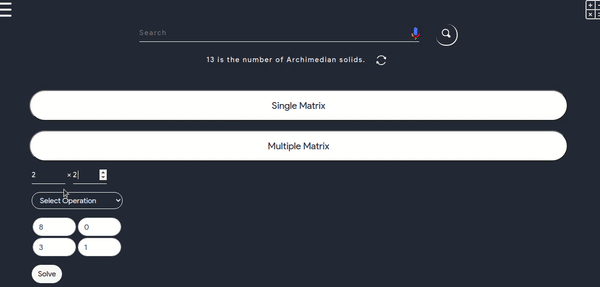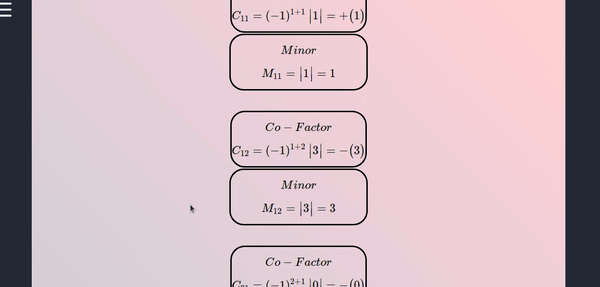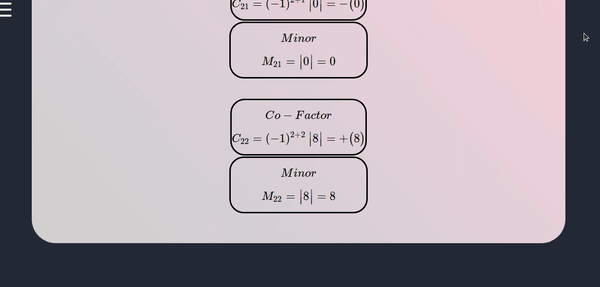
How to use this tool for single matrix

• This tool can be used for any order of single matrix where we can perform different operations such as Transpose of a matrix, determinant of matrix, minors and co-factors of a matrix, plus this tool gives you the step by step notes at the same time, below is a demo

Operations on multiple matrices

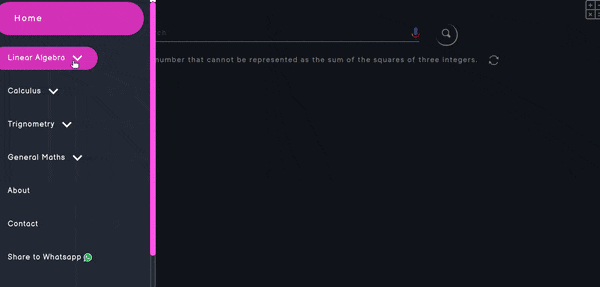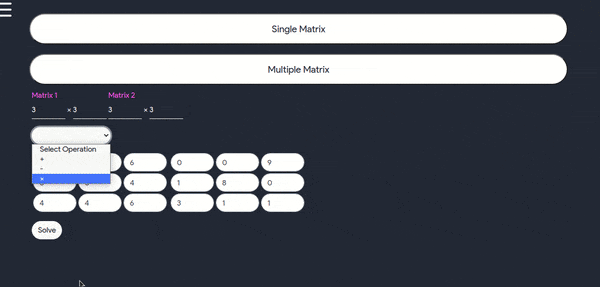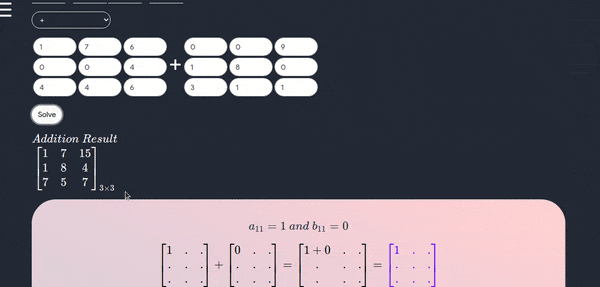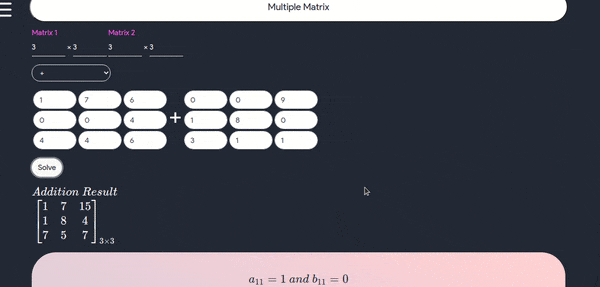
• Addition and Subtraction
  • Two matrices may be added or subtracted only if they have the same dimension; that is, they must have the same number of rows and columns.
  • Addition or subtraction is accomplished by adding or subtracting corresponding elements. For example, consider matrix A and matrix B.

$$ \begin{equation}A = \begin{bmatrix} 1 & 2 & 3 \\ 7 & 8 & 9 \\ \end{bmatrix} B\enspace = \begin{bmatrix} 5 & 6 & 7 \\ 3 & 4 & 5 \\ \end{bmatrix} \end{equation} $$

$$ \begin{equation}A + B = \begin{bmatrix} 1+5 & 2+6 & 3+7 \\ 7+3 & 8+4 & 9+5 \\ \end{bmatrix} = \begin{bmatrix} 6 & 8 & 10 \\ 10 & 12 & 14 \\ \end{bmatrix} \end{equation} $$

.

• Similary you can subtract two or may be more matrices like this
• To understand matrix addition, subtraction and multiplication better,input any example and examine the solution.

How to use this tool for Multiple matrix

• This tool can only be used for two matrices for any order where we can perform different operations such as addition, subtraction and multiplication, plus this tool gives you the step by step notes at the same time, below is a demo

Cayley Hamilton Theorem and Diagonalization

• every square matrix over a commutative ring (such as the real or complex field) satisfies its own characteristic equation.

• A square matrix can be written as

  A- λI

  =0 and the corresponding eqn is

$$ A^m + c_{m-1} A^{m-1} + ... + c_{0}I = 0 $$

• The cayley-hamilton theorem states that an nxn matrix A is ahhihilated by its characteristic polynomial det(A) , which is monic of degree n
• The Cayley–Hamilton theorem states that substituting the matrix A for x in polynomial, p(x) = det(xIn – A), results in the zero matrices, such as:
• p(A) = 0
• It states that a ‘n x n’ matrix A is demolished by its characteristic polynomial det(tI – A), which is monic polynomial of degree n.
• The powers of A, found by substitution from powers of x, are defined by recurrent matrix multiplication; the constant term of p(x) provides a multiple of the power A0, where power is described as the identity matrix.
• The theorem allows An to be articulated as a linear combination of the lower matrix powers of A.
• If the ring is a field, the Cayley–Hamilton theorem is equal to the declaration that the smallest polynomial of a square matrix divided by its characteristic polynomial.

Diagonalization of Matrix

• Matrix diagonalization is the process of taking a square matrix and converting it into a special type of matrix–a so-called diagonal matrix–that shares the same fundamental properties of the underlying matrix.
• Matrix diagonalization is equivalent to transforming the underlying system of equations into a special set of coordinate axes in which the matrix takes this canonical form.
• Diagonalizing a matrix is also equivalent to findingthe matrix’s eigenvalues, which turn out to be precisely the entries of the diagonalized matrix.
• Similarly, the eigenvectors make up the new set of axes corresponding to the diagonal matrix.
• The remarkable relationship between a diagonalized matrix, eigenvalues, and eigenvectors follows from the beautiful mathematical identity (the eigen decomposition) that a square matrix A can be decomposed into the very special form

A = PDP^{-1}

• D is the diagonalized matrix and can be written as diagoanl matrix containing eigen values on the major diagonal

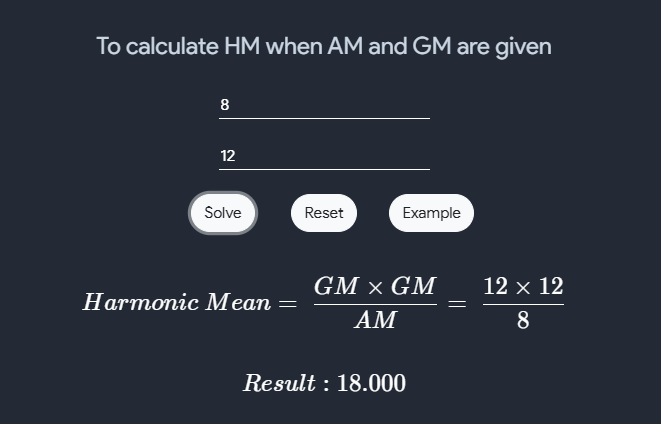
Mean Calculator

• this tool have 4 calcualtors, following are the calculators

1. Arithmetic Mean

1. Geometric Mean

1. Harmonic Mean

1. Harmonic Mean using AM and GM

Sequence & Series

Arithmetic Progression

• A mathematical sequence in which the difference between two consecutive terms is always a constant and it is abbreviated as AP.

• Notion in AP
  • In AP, we will come across three main terms,which is denoted as:
    • common difference (d)
    • nth term (an)
    • Sum of the first n terms \(s_{n}\)
• Common Difference in AP
  • in this progression for a given series , the terms used are the first term, the commond differnence between the two terms and the nth term
  • suppose a1,a2,a3,…..,an is an AP, then the common difference is “d” can be obtained as d = a2-a1 = a3-a2 etc
  • Where ‘d’ is a common difference
  • it can be +ve,-ve or 0
• First term of AP
  • the AP can also be written in terms of common difference as follows; a,a+d,a+2d,a+3d,a+4d+….+a+(n-1)d
  • where ‘a’ is the first term of the progression
• nth term of an ap
  • \[a_{n} = a+ (n-1) * d\]
  • where a = first term, d = common difference
  • n = number of terms and an = nth term
• sum of N terms of AP
  • For any progression the sum of n terms can be easily calculated
  • for AP, the sum of the first n terms can be calculated if the first term and the total terms are known
  • The formula for the arithmetic progression sum is explained below
  • conside an AP consisting of ‘n’ terms then
  • \[s = \dfrac{n}{2} (2a + (n-1) x d)\]
• Sum Of AP when the last term is given
  • Formula to find the sum of AP when first and last term are given as follows
  • \[S = \dfrac{n}{2} (first term + last term)\]

Geometric Progression

• if in a sequence of terms , each succeeding term is generated by multiplying each preceding term with a constant value, then the sequence is called a geometric progression
• GP, whereas the constant value is called the common ratio
• for example : 2,4,8,16,24,64… is a GP, where common ration is 1
• A sequence a1,a2,a3,…,an is a GP then
• \[\dfrac{a_{k+1}}{a_{k}} =r where k > 1\]
• Sum of Nth terms of GP
  • consider the \(GP 1,ar,ar^2 ,..., ar_{n-1}\)
  • let sn,a,r be the sum of n terms, first term and common ratio of GP, respectively
  • then \(S_{n} = \dfrac{a(n^{n-1}-1)}{r-1}\)
• Sum to infinity of GP
  • if the number of terms in a GP is not finite, then the GP is called infinite GP
  • The formula to find the sum of infinity of the given GP is \(S_{\infty} = \sum_{n-1}^{infty} ar^{n-1} = \dfrac{a}{1-r}; -1< r < 1\)

Sum of N terms of AP,GP and HP

• This section of AP,GP and HP contains many calculators and they are

  • Sum of N terms of an AP

    • 

  • if first term,number of terms and last term is given

    • 

  • Insert n-arithmetic mean between two numbers

    • 

  • If number of terms and the AP is given

    • 

  • Sum of p terms of an AP if mth and nth term are given

    • 

  • Ratio of mth and nth terms of an AP

    • 
  • Constant/Increasing/Decreasing AP
  • Three Consecutive Term (AP,GP or HP)
  • Sum of N terms of a geometric progression
  • Sum of infinite of a geometric progression with common ration less than 1
  • Sum of P terms of an GP if mth and nth terms are giveb
  • Sum of N terms of a harmonic progression
  • harmonic progression
  • Harmonic Progression nth term from end and etc many more

Aliquot Sum

• In number theory, the aliquot sum s(n) of a positive integer n is the sum of all proper divisors of n, that is, all divisors of n other than n itself.
• this tool includes various calculators and they are:
  • Aliquot sum s(n) of a positive integer n is the sum of all peoper divisors of n, that is all divisors of n other than itself
  • Primitive Abundant Number
  • Check if a number can be expressed as sum of two abundant number
  • Hosoya’s Triangle
  • Cassini’s Identity

Golden And Silver Ratio

• Golden Ratio : In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities.
• Silver Ratio : In mathematics, two quantities are in the silver ratio if the ratio of the smaller of those two quantities to the larger quantity is the same as the ratio of the larger quantity to the sum of the smaller quantity and twice the larger quantity.
• This tool includes various calculators
  • Check wheter two numbers are in golden ratio
  • Find nth fibonacci number using Golden ratio
  • Check whether two numbers are in silver ratio

Types of Relations

• Sets and relation are interconnected with each other. The relation defines the relation between two given sets. If there are two sets available, then to check if there is any connection between the two sets,we use relations For example, An empty relation denotes none of the elements in the two sets is same.
• There are 8 main types of relations which include:
  • Empty Relation

    • An empty relation (or void relation) is one in which there is no relation between any elements of a set. For example, if set A = {1, 2, 3} then, one of the void relations can be R = {x, y} where,

      x – y

      = 8. For empty relation, R = φ ⊂ A × A

  • Universal Relation

    • A universal (or full relation) is a type of relation in which every element of a set is related to each other. Consider set A = {a, b, c}. Now one of the universal relations will be R = {x, y} where,

      x – y

      ≥ 0. For universal relation, R = A × A

  • Identity Relation
    • In an identity relation, every element of a set is related to itself only. For example,in a set A = {a, b, c}, the identity relation will be I = {a, a}, {b, b}, {c, c}. For identity relation,I = {(a, a), a ∈ A}
  • Inverse Rwaltion
    • Inverse relation is seen when a set has elements which are inverse pairs of another set. For example if set A = {(a, b), (c, d)}, then inverse relation will be R inverse = {(b, a), (d, c)}. So, for an inverse relation,
  • Reflexive Realtion
    • In a reflexive relation, every element maps to itself. For example, consider a set A = {1, 2,}. Now an example of reflexive relation will be R = {(1, 1), (2, 2), (1, 2), (2, 1)}. The reflexive relation is given by- (a, a) ∈ R
  • Symmetric Realtion
    • In a symmetric relation, if a=b is true then b=a is also true. In other words,a relation R is symmetric only if (b, a) ∈ R is true when (a,b) ∈ R. An example of symmetric relation will be R = {(1, 2), (2, 1)} for a set A = {1, 2}. So, for a symmetric relation, aRb ⇒ bRa, ∀ a, b ∈ A
  • Transitive Relation
    • For transitive relation, if (x, y) ∈ R, (y, z) ∈ R, then (x, z) ∈ R. For a transitive relation, aRb and bRc ⇒ aRc ∀ a, b, c ∈ A
  • Equivalence Relation
    • If a relation is reflexive, symmetric and transitive at the same time it is known as an equivalence relation.

Sets Formulas

$$ if \enspace A \enspace and \enspace B \enspace are \enspace overlapping \enspace sets \enspace n(A\cup B) = n(A) + n(B) - n(A \cap B) $$ $$ If A \enspace and \enspace B \enspace are \enspace disjoint \enspace sets \enspace n (A\cup B) = n(A) + n(B) $$ $$ n(A) = n(A\cup B) + n(A\cap B) - n(B) $$ $$ n(A\cap B) = n(A) + n(B) -n(A\cup B) $$ $$ n(B) = n(A\cup B) + n(A\cap B) -n(A) $$ $$ n(U) = n(A) + n(B) - n(A\cap B) + n((A\cup B)^c) $$ $$ n((A\cup B)^c) = n(U) + n(A\cap B) - n(A)- n(B) $$ $$ n(A\cup B) = n(A-B) + n(B-A) + n(A\cap B) $$ $$ n(A-B) = n(A \cup B) - n(B) $$ $$ n(A-B) = n(A) - n(A\cap B) $$ # Sigma Notaion - $$ \sum $$ is a letter of greek alphabets and it is called sigma. the symbol sigma represents the sum of similar term. - properties of sigma notation

$$ \sum_{r=1}^{n} T_{r} + T1 + T2 + T3 + ....+ Tn , where \enspace T_{n} \enspaceis \enspace the \enspace general \enspace term \enspace of \enspace the \enspace series $$ $$ \sum_{r=1}^{n} T_{r} \plusmn T_{r}^' = \sum_{r=1}^{n} T_{r} T_{r} \plusmn \sum_{r=1}^{n} T_{r}^' $$ $$ \sum_{r=1}^{n} T_{r} T_{r}^' = (\sum_{r=1}^{n} T_{r})(\sum_{r=1}^{n} T_{r}^') $$ $$ \sum_{r=1}^{n} \dfrac{T_{r}}{T_{r}^'} ! = \dfrac{\sum_{r=1}^{n} T_{r}}{\sum_{r=1}^{n} T_{r}^'} $$ $$ \sum_{r=1}^{n} aT_{r} = a \sum_{r=1}^{n} aT_{r} $$

Creamers Rule

• In linear algebra, Cramer’s rule is an explicit formula for the solution of a system of linear equations with as many equations as unknowns, valid whenever the system has a unique solution.
• It expresses the solution in terms of the determinants of the (square) coefficient matrix and of matrices obtained from it by replacing one column by the column vector of right-hand-sides of the equations.

Mathematical Reasoning

• Difference between statement and sentence in logic
  • A statement is a sentence which is either true or false but not true and false simultaneously
  • A sentence will not be considered to be a statement if : it is an exclamation, order, request, depicts time, places , pronouns
• Simple Statement
  • If a statement cannot be further broken down into various statements, or in simpler words if it is concrete by itself, it is called a simple statement
• Compound Statement
  • If a statement can further be broken down into simpler statements os that from a main statement, we can yeild more than one statement, then it is called a compound statement
• Conjuction, Disjunction and Negation
  • CONJUNCTION
    • The statement \(p^q\) has the truth value T(true) if both p and q have the truth value T.
    • similarly, the statement \(p^q\) has the truth value F(flase) if either p or q have the truth value F or both have the truth value F.
  • DISJUNCTION
    • The statement pvq has the truth value F(value) if bothh p and q have truth value F.
    • Similarly, the statement pvq has the truth value T(true) if either p or q have the truth value T or both have the truth value T
  • NEGATION
    • p has truth value T whenever p has truth value F.
    • p has truth value F whenever p has truth value T.
• AND OPERATION:

P	Q	P^Q
T	T	T
T	F	F
F	T	F
F	F	F

• OR OPERATION:

P	Q	PvQ
T	T	T
T	F	T
F	T	T
F	F	F

• NEGATION:

P	~P
T	F
F	T

Euclid Geometry

• Euclid Axioms
  • There are 7 axioms in euclid geometry
    • thing which are equal to the same thing are equal to one another
    • if equal are added to equals, the wholes are equal
    • if equal are subtracted from equals, the remaiunde are equal
    • things which coincide with one another are equal to one another
    • the whole is than the part
    • things which are double of the same things are equal to another
    • Things which are halves of the same things are equal to one another
  • Euclid’s Postulates
    1. A straight line can be drawn from anyone point to another point
    2. A terminated line can e further produced inside finitely
    3. A circle can be drawn with any center and any radius.
    4. all right angles are equal to one another
    5. if a straight line falling on two other stright lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced inde finitely, meet on the side on which the sum of angles is less that two right angles.

Sets , Relations and Functions

What are sets

• A set is the representation of a collection of objects; distinct objects with one or more common properties.

• Types of sets
  • Empty Set - A set with no elements. Empty sets are also called null sets or void sets and are denoted by { } or Φ.
  • Singleton Set - A set with a single element. For example, {9}.
  • Power Set - A set qualifies asthe subset of another set if all of its elements are also the elements of that another set. A collection of all the subsets of a given set is a power set.
  • Super Set - A super-set can be thought of as the parent set that at least contains all the elements of the subset and may or may not contain some extra elements.
• What are relations and functions
  • Relations and functions are the set operations that help to trace the relationship between the elements of two or more distinct sets or between the elements of the same set.
  • The relation is the subset of the Cartesian product which contains only some of the ordered pair based on the relationships defined between the first and second elements. The relation is usually denoted by R.
  • If every element of a set A is related with one and only one element of another set then this kind of relation qualifies as a function. A function is a special case of relation where no two ordered pairs can have the same first element.

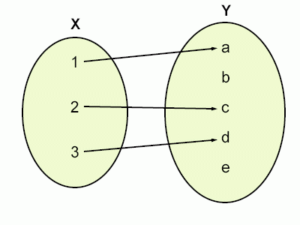
• Conditions to be a function

  • A relation from a set X to a set Y is called a function if each element of X is related to exactly one element in Y. That is, given an element x in X, thereis only one element in Y that x is related to.

• Operations on Sets
• Union
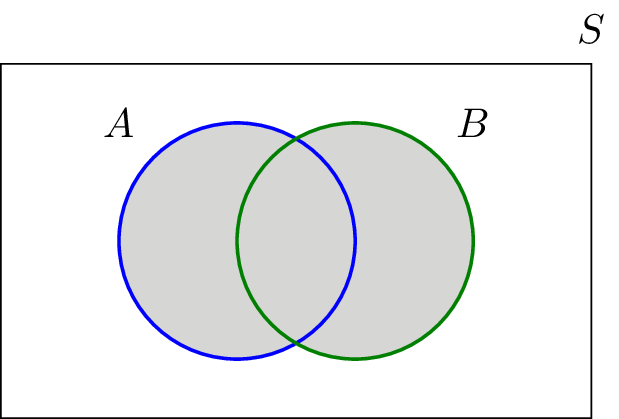
  • The union of two sets is a set containing all the elements that are in A or in B (Possibly Both). For example \({1,2} \cup {2,3} = {1,2,3}\)
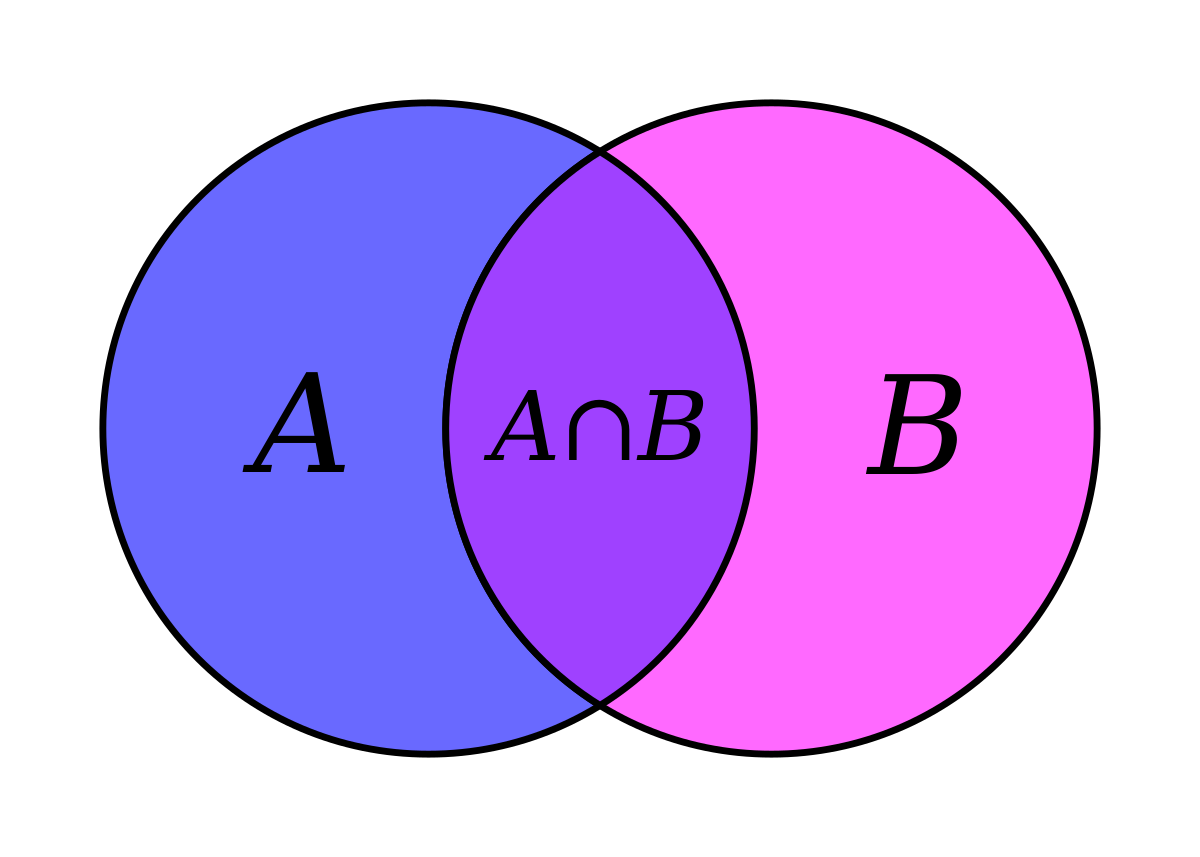
• Intersection
  • The intersectionof two sets A and B, denoted by \(A \cap B\) consists of all elements that are both in A and B, for example \({1,2} \cap {2,3} = {2}\)

  

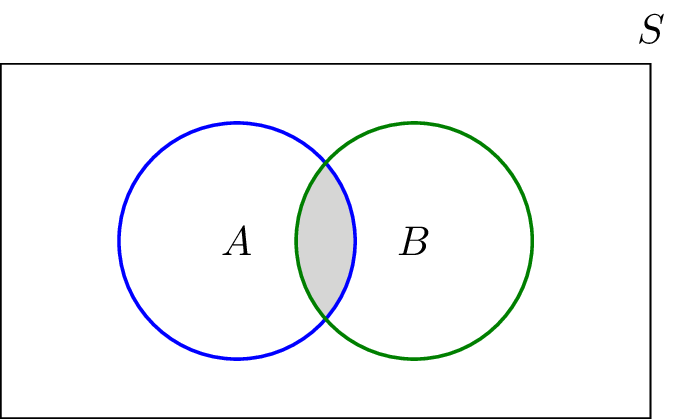
  • the intersection of A and B is the middle part

  

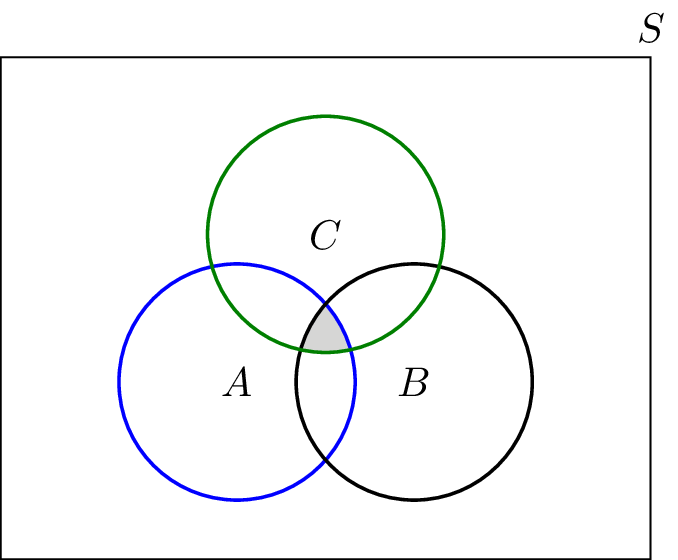
• Disjoint
  • Set A and Set B are called disjoint sets if no elements is common to A and B i.e A and B are joint sets then \(a \cap B = \theta\)
  • \[A = {1,3,5} , B = {2,4,6} and C = {a,b,c} , A \cap B \cap C = \theta\]

  

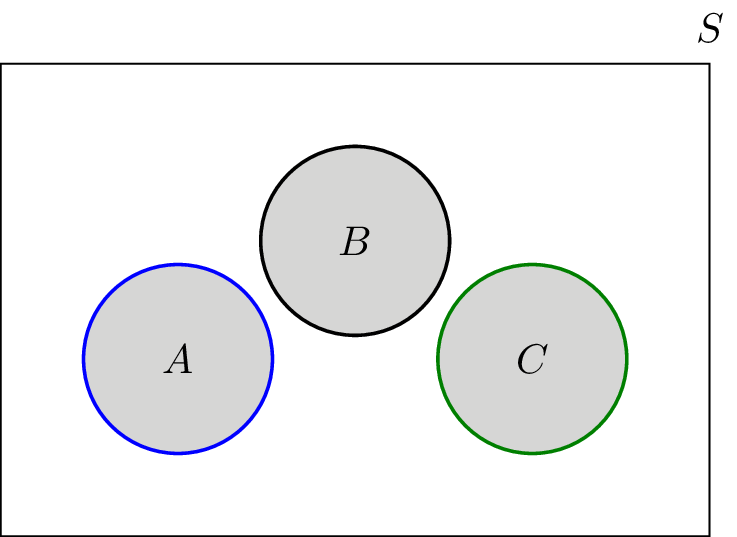
• Complement
  • The complement of set A , denoted by A is elements in universal Set which are not in A

  

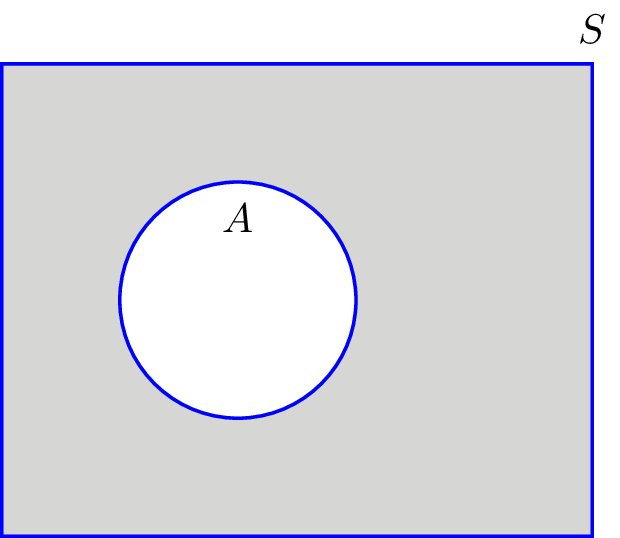
• Difference
  • The set A - B consists of elements that are in A but not in B, for example if \(A = {1,2,3} and B = {3,5} then , A - B = {1,2}\)

  

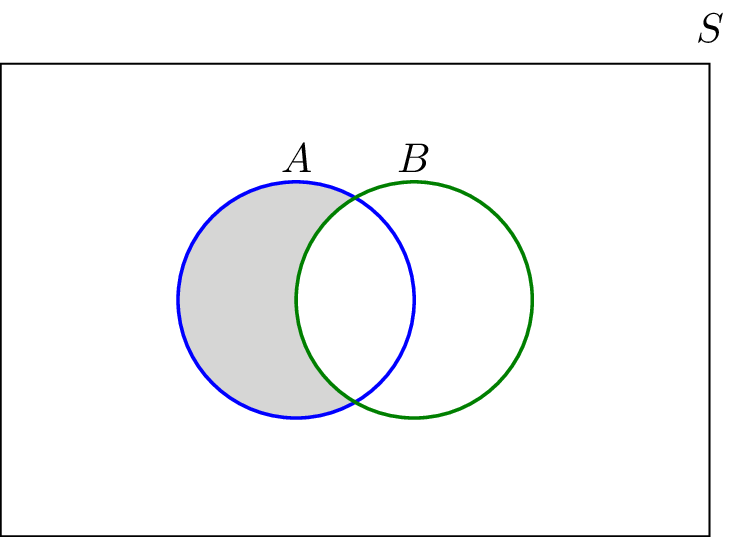
  • Types of Functions
    • One to one function(Injective): For each element in the domain there is one and only one element in the range.
    • Many to one function: When two or more elements from the domain are mapped to the same single elements in the range.
    • Onto function(Surjective): When every element of the range has been mapped to an element in the domain.
    • One-one and onto function(Bijective): A function which is both one to one and onto function.