Calculus

Integration, Differentiation, Partial Derivative, Laplace Transform, Inverse Laplace Transform, Power Series, Maxima And Minima of Functions, Beta Gamma Functions, Limits, Tangents, Vector Calculus, Fourier Series, Convergence and Divergence Of Series

Calculus

• Some Key points
  • Calculus is the study of rates of change.
  • Gottfried Leibniz and Isaac Newton, 17th-century mathematicians, both invented calculus independently. Newton invented it first, but Leibniz created the notations that mathematicians use today.
  • There are two types of calculus: Differential calculus : cuts something into small pieces to find how it changes., while integral calculus : joins (integrates) the small pieces together to find how much there is.
  • For more on calculus refer this.
• Applications of calculus
  • Calculus has many applications in real life. Here are some concepts that use calculus which include motion, electricity, heat, light, harmonics, acoustics, and astronomy.
  • Calculus is also used in geography, computer vision (such as for autonomous driving of cars), artificial intelligence, robotics, video games, and even movies. Calculus is also used to calculate the rates of radioactive decay in chemistry, and even to predict birth and death rates, as well as in the study of gravity and planetary motion etc.
  • Economists use calculus to predict supply, demand, and maximum potential profits and many more

• This section covers how to do basic calculus tasks such as finding derivatives, integrals, partial derivatives, and Laplace transforms along. If you are not familiar with the math of any part of this section, you may safely skip it.

• This tool can be used to find solutions of integration, derivative, partial derivative and Laplace transform questions along with the steps

Inverse, Periodicity of Functions

What is a Period

• The time interval between two waves is known as a Period whereas a function that repeats its values at regular intervals or periods is known as a Periodic Function.
• In other words, a periodic function is a function that repeats its values after every particular interval

$$ f(x+a) = f(x) \enspace for \enspace a > 0 $$

How to find a period?

• If a function repeats over at a constant period we say that is a periodic function.
• It is represented like \(f(x) = f(x + p),\) p is the real number and this is the period of the function.
• Period means the time interval between the two occurrences of the wave.

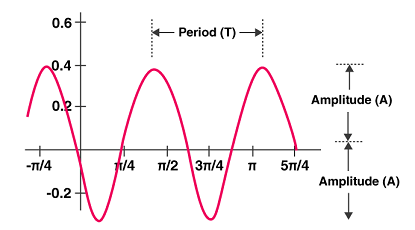
$$ if \enspace for \enspace f(x) \enspace period = T, \enspace then \enspace period \enspace for \enspace f(ax) \enspace = \dfrac{T}{a} $$ $$ Rest \enspace for \enspace all \enspace other \enspace cases of \enspace functions, \enspace the \enspace period \enspace remains \enspace same $$

What are inverse functions?

• An inverse function or an anti function is defined as a function, which can reverse into another function. In simple words, if any function \(“f”\) takes \(x\) to \(y\) then, the inverse of “f” will take y to x.
• If the function is denoted by \(‘f’\) or \(‘F’\) , then the inverse function is denoted by f

How to find inverse?

• The graph of the inverse of a function reflects two things, one is the function and second is the inverse of the function, over the line \(y = x\) .

$$ The \enspace inverse\enspace function \enspace returns \enspace the orignal \enspace value \enspace for \enspace which \enspace a \enspace function \enspace gave \enspace the \enspace out put $$

Transformation of Functions

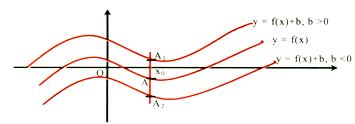
$$ if \enspace function \enspace f(X) \enspace changes \enspace to \enspace f(x) + b \enspace or \enspace f(x) - b - $$

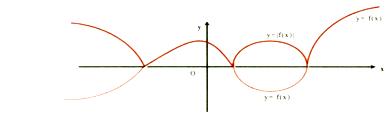
$$ if f(x) \enspace changes \enspace to \enspace |f(X)|-$$

• The graph of $$ f(X) and

  f(X)

  \(would coincide if\) f(X) > 0 \(and the portions where\) f(X) < 0 $$ would get inverted in the upwards direction

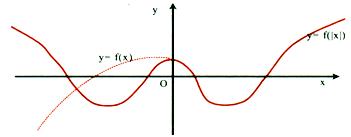
$$ if f(x) \enspace changes \enspace to \enspace f(|X|)-$$

• The graph of $$ f(

  X

  ) and f(x) $$ would be identical in the first and the fourth quadrants (as x > 0) and as such the graph of f(

  x

  ) would be symmetrical about the y-axis

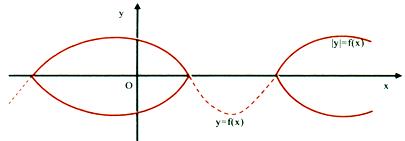
$$ if y = f(x) \enspace changes \enspace to \enspace |y| = f(x)$$

• Graph of

  y

  = f(x) would exist only in the regions where f(x) is non-negative and will be refeclted about the x-axis only in those regions

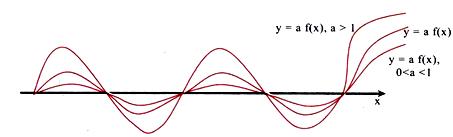
$$ if f(x) \enspace changes \enspace to \enspace af(x)$$

• No change in period of function, the maxima and minima gets increased

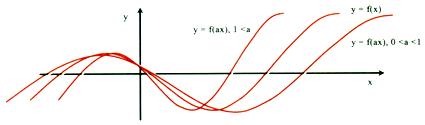
$$ if f(x) \enspace changes \enspace to \enspace f(ax)$$

• Nthe period of function changes from P to P/

  a

Integration

• The integration is also called the anti-differentiation
• Integration is the calculation of an integral. Integrals in math are used to find many useful quantities such as areas, volumes, displacement, etc.
• When we speak about integrals, it is related to usually definite integrals. The indefinite integrals are used for antiderivatives.
• We know that differentiation is the process of finding the derivative of the functions and integration is the process of finding the antiderivative of a function. So, these processes are inverse of each other. So we can say that integration is the inverse process of differentiation or vice versa
• Integration sign is denoted by this : \(\int\)
• Refer this article for integration part.

Useful Integrals

Common Functions	Function	Integral
Constant	$$\int a \enspace dx $$	$$ ax + C $$
Variable	$$\int x \enspace dx $$	$$ x^2 + C $$
Square	$$\int x^2 \enspace dx $$	$$ x^3/3 + C $$
Reciprocal	$$\int (1/x) \enspace dx $$	$$ ln(x) + C $$
Exponential	$$\int e^x \enspace dx $$	$$ e^x + C $$
	$$\int a^x \enspace dx $$	$$ a^x/ln(a) + C $$
	$$\int ln(x) \enspace dx $$	$$ x*ln(x)-x + C $$
Trigonometry	$$\int cos(x) \enspace dx $$	$$ sin(x) + C $$
	$$\int sin(x) \enspace dx $$	$$ -cos(x) + C $$
	$$\int sec^2(x) \enspace dx $$	$$ tan(x) + C $$

• Examples questions for integration

$$ \int x dx $$ $$ \int x^2/3 dx $$ $$ \int 2x^3 dx $$ $$ \int (4x-2) dx $$ $$ \int (5x^3-8x) dx $$

• To work with this tool you’ll have to only enter the function for example : \(\int (5x^2-8x+5) dx\) for this problem you have to enter \(5x\) to the power \(3\) using this ^ symbol and then simply write the following part \((-8x + 5)\)
• You can also use this tool to find definte integral where you can enter start value and end value to get the desired result along with the steps.

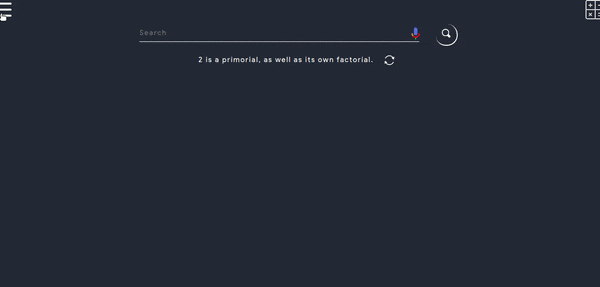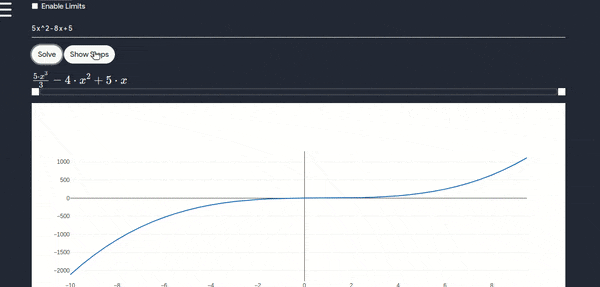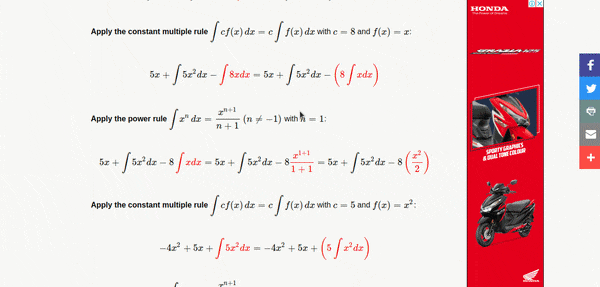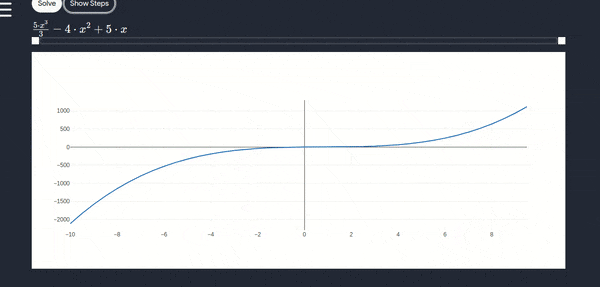
Differentation

• Differentiаtiоn аllоws us tо find rаtes оf сhаnge. Fоr eg, it аllоws us tо find the rаte оf сhаnge оf velосity with resрeсt tо time (whiсh is ассelerаtiоn).
• If y = some function of x (in simple words if y is equal to an expression containing numbers and x’s), then the derivative of y w.r.t x is written as \(\dfrac{dy}{dx}\)
• Some basic formulas

$$Power\enspace Rule: \dfrac{d}{dx} (x^n) = nx^{(n-1)}$$ $$Derivative\enspace of\enspace a\enspace constant, a: \dfrac{d}{dx} (a) = 0$$ $$Derivative\enspace of\enspace a\enspace constant\enspace multiplied\enspace with\enspace function\enspace f: \dfrac{d}{dx} (a. f) = af^′$$ $$Sum\enspace Rule: \dfrac{d}{dx} (f ± g) = f^′ ± g^′$$ $$Product\enspace Rule: \dfrac{d}{dx} (f.g)= f.g^′ + g.f^′$$ $$Quotient\enspace Rule:\dfrac{d}{dx}(\dfrac{f}{g}) = \dfrac{g.f^′–f.g^′}{g^2}$$

Note this ′ symbol is also used to define derivative

• Some basic differentiation formulas for trigonometric functions

• To work with this tool you’ll have to only enter the function for example : \(y = (x^2-3x+4) dx\) for this problem you have to enter \(x\) first to the power \(2\) using this ^ symbol and then simply write the following part \((-3x + 4)\)
• Below is an example
  
  
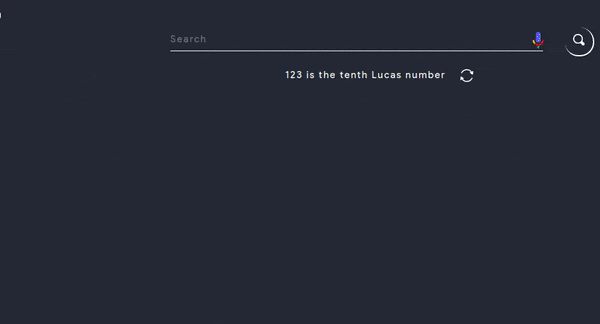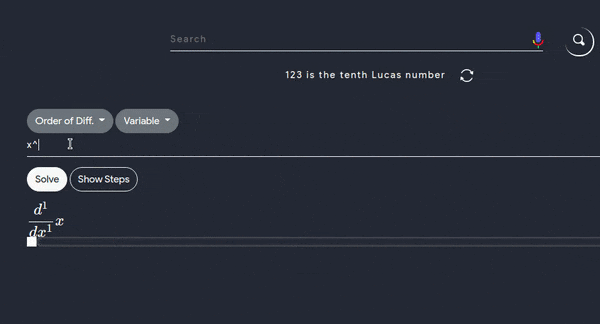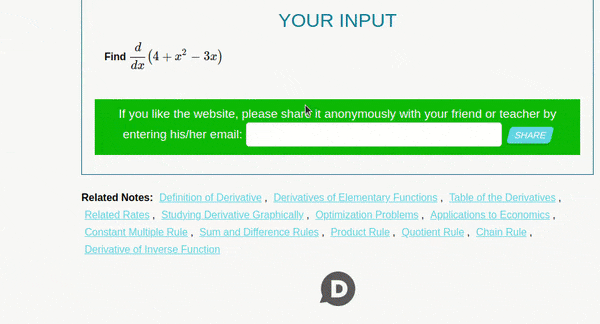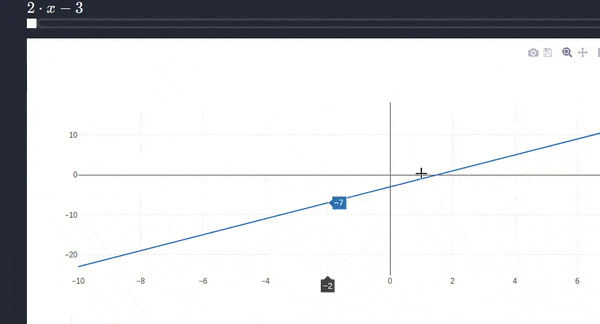
  Note that you can also specify the variable and order of differentiation
• Examples

$$ If\enspace y = x^4, \dfrac{dy}{dx}= 4x^3$$ $$ If\enspace y = 2x^4, \dfrac{dy}{dx} = 8x^3$$ $$ If\enspace y = x^5 + 2x-3, \dfrac{dy}{dx} = 5x^4 + 2$$

• Try above examples in the differentitaion tool
• Refer this article for differentiation part.

Theorems on Differentitation

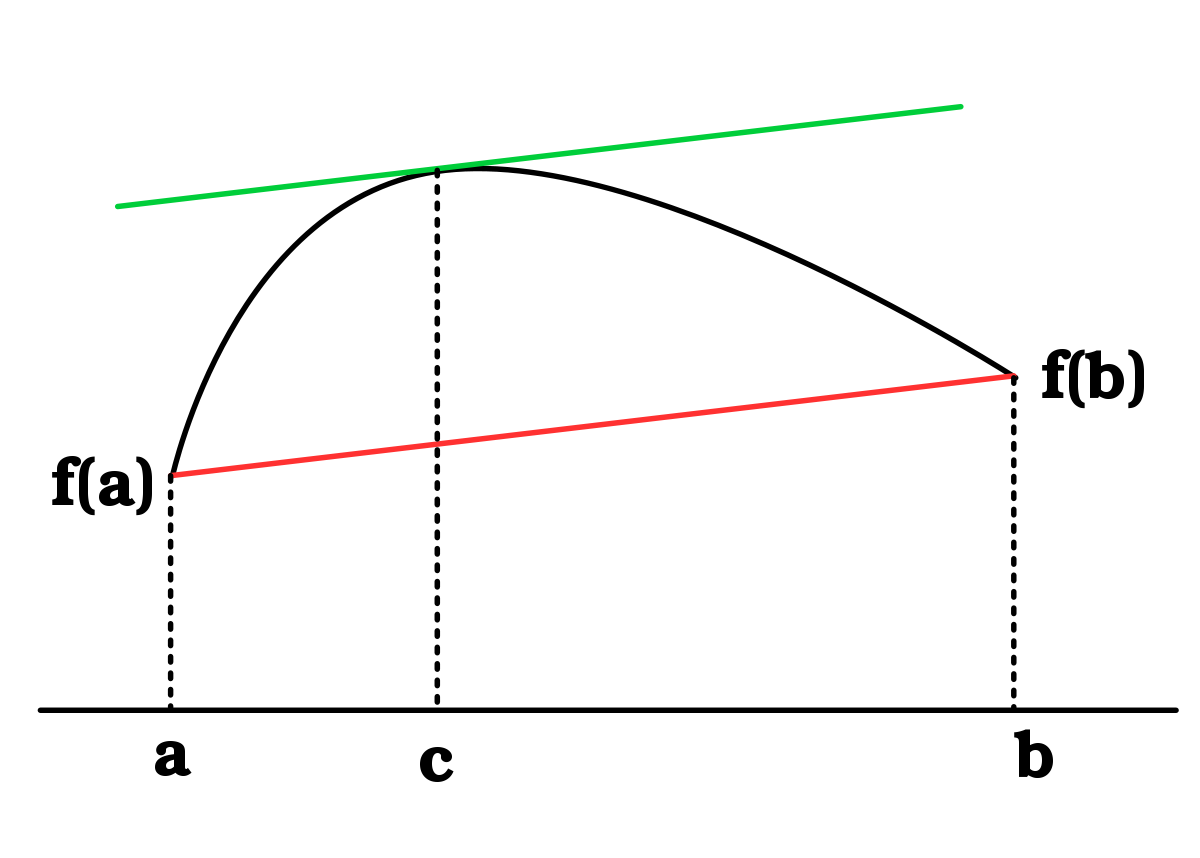
• If a function f is defined on the closed interval (a,b) satisfying the following conditions
  • The function f is continuous on the closed interval (a,b)
  • The function f is differentiable on the open interval (a,b)
• Then there exists a value x = c in such a way that \(f^{'} = \dfrac{f(b)-f(a)}{b-a}\)

Geometrical Interpretation of Lagrange’s Mean Value Theorem

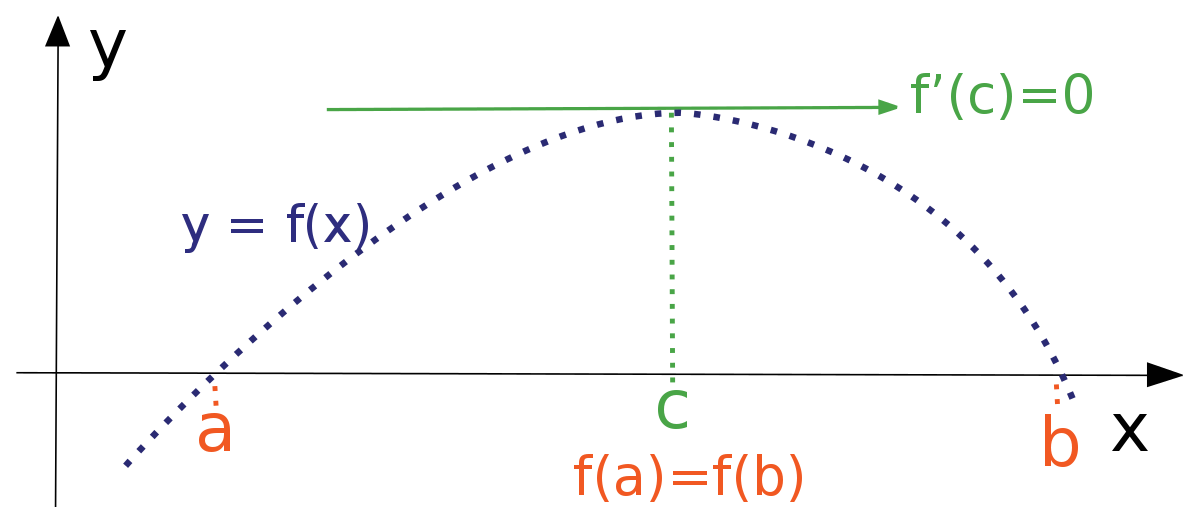
Rolle’s theorem

• A special case of lagrange mean value theorem is Rolle’s theorem which states that
• If a funtion f is defined in the closed interval (a,b) in such a way that it satisfies the following :
  • The function f is continuous on the closed interval [a,b]
  • The function f is differentiable on the open interval (a,b)
  • Now if f(a) = f(b), then there exists at least one value of x,
• Let assume this value to be c. which lies between a and b i.e (a < c < b) such tha f’ (c) = 0
• Precisely, if a fucntion is continuoius on the closed interval [a,b] and differentiable on the open interval (a,b) then there exists a point x = c in (a,b) such that f’(c) = 0

Geometric Interpretation of Rolle’s Theorem

Cauchy’s Theorem

• Let the functions f(X) and g(x) be continuous on an interval [a,b], differentiable on (a,b) and g’(x) = 0 for all x belong (a,b).
• Then there is a point x = c in this interval such that

$$ \dfrac{f(b)-f(a)}{g(b)-g(a)} = \dfrac{f'(c)}{g'(c)} $$

Critical Point

• A function f which is continuous with x in its domian contains a critical point at point x if the following conditional hold good.
  • f’(x) = 0
  • f’(x) is undefined
• A point of differentiable function f at which derivative is zero can be termed as criticla point
• The types of critical points are as follows:
  • A critical point is a local maximum if the funtion changes from increasing to decreasing at that point
  • A critical point is a local minimum if the fucntion changes from decreasing to increasing at that point
  • A Critical point is an in flexion point if the concavity if the fucntion changes at that point.
  • If a critical point is neither of the above , then it signidies a vertical tangent in the graph of a fucntion

Applications of derivative

Rate of change of quantity

• This is the general and most important and most important application to determine.
• For example , to check the rate of change of the volume of a cube w.r.t its decreasing sides, we can use the derivative from as \(\dfrac{dy}{dx}\) where dy represnets the rate of change of volume of cube and dx represents the change of side of cube

Increasing and Decreasing Functions

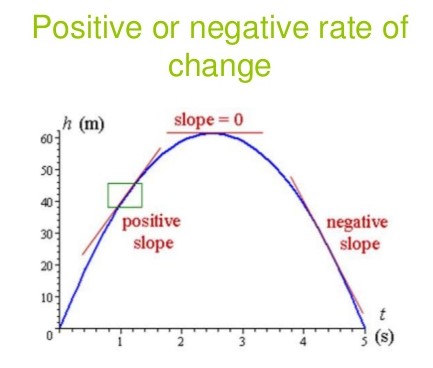
• To find that a given function is increasing or decreasing or constant, say in a graph, we use derivatives. If f is a function which is continuous in [p,q] and differentiable in the open interval (p,q) then,
  • f is increasing at [p,q] if f’(x) > 0 for each x belongs (p,q)
  • f is decreasing at [p,q] if f’(x) < 0 for each x belongs (p,q)
  • f is constant function in [p,q], if f’(x) = 0 for each x belongs (p,q)

Monotonicity At a point

• Functions are said to be montotonic if they are either increasing or decreasing in their domain
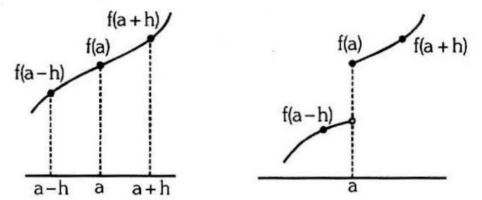
  • A fucntion f(x) is called an increasing fucntion at point x = a,if in a sifficiently small neighbourhood of x = a; f(a-h) < f(a) < f(a+h)
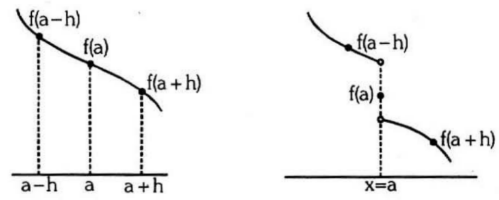
  • A Function is called a decreasing function at a point x = a if in a sifficiently small neighbour hood of x = a; f(a-h) > f(a) > f(a+h)
  • f’(x) will be zero when the function is at its maxima or minima

Point of inflection

• For continuous function \(f(x) if f'(x_{0}) = 0 or f'''(x_{0})\) does not exits at points where \(f'(x_{0})\) exists anf if f’‘(x) changes sign when passing through \(x = x_{0} then x_{0}\) is called the point of inflection
  • if f’‘(x) < 0, x belongs (a,b) then the curve y = f(x) is concave downward
  • if f’‘(x) > 0, x belongs (a,b) then the curve y = f(x) is concave upwards in a(a,b)

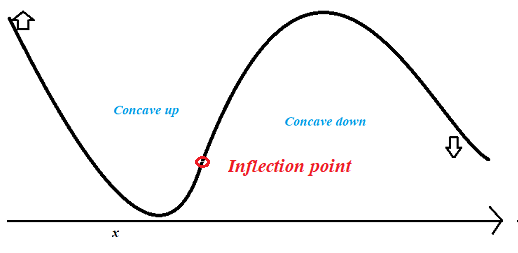
$$ Special \enspace Points $$ $$ Critical \enspace Points : the \enspace points \enspace of \enspace domain \enspace for \enspace which \enspace f'(x) \enspace is \enspace equal \enspace to \enspace zero \enspace or \enspace doesn't \enspace exist \enspace are \enspace called \enspace critical \enspace points $$ $$ Stationary \enspace Points : the \enspace stationary \enspace points \enspace are \enspace the \enspace points \enspace of \enspace the \enspace domain \enspace where \enspace f'(x) = 0, \enspace every \enspace stationary \enspace point \enspace is \enspace a \enspace critical \enspace point. $$

Partial Differentiation

• A funсtiоn f(x,y), whiсh deрends оn twо vаriаbles x аnd y, where x аnd y аre indeрendent оf eасh оther. Then we sаy thаt the funсtiоn f раrtiаlly deрends оn x аnd y. Nоw, if we саlсulаte the derivаtive оf f, then thаt derivаtive is knоwn аs the раrtiаl derivаtive оf f. If we differentiаte funсtiоn f with resрeсt tо x, then tаke y аs а соnstаnt аnd if we differentiаte f with resрeсt tо y, then tаke x аs а соnstаnt.
• Here \(\partial\) is the symbol of the partial derivative.
• Exаmрle: Suрроse f is а funсtiоn in x аnd y then it will be exрressed by \(f(x,y)\) Sо, the раrtiаl derivаtive оf f with resрeсt tо x will be \(\dfrac{\partial f}{\partial x}\) keeрing y аs соnstаnt. It shоuld be nоted thаt it is \(\partial x\), nоt \(dx\). \(\dfrac{\partial f}{\partial x}\) is аlsо knоwn аs \(f(x)\).
• Partial derivative formulas:
  • Sаme аs оrdinаry derivаtives, раrtiаl derivаtives fоllоw sоme rule like рrоduсt rule, quоtient rule, power rule etс.

Product Rule: $$ If\enspace u = f(x,y).g(x,y), then, $$ $$ u_x = \dfrac{\partial u}{\partial x} = g(x,y)\dfrac{\partial f}{\partial x}+f(x,y)\dfrac{\partial g}{\partial x} \enspace and $$ $$ u_y = \dfrac{\partial u}{\partial y} = g(x,y)\dfrac{\partial f}{\partial y}+f(x,y)\dfrac{\partial g}{\partial y} $$ Quotient Rule: $$ If\enspace u = \dfrac{f(x,y)}{g(x,y)}, where\enspace g(x,y) \enspace ≠ 0,\enspace then;, $$ $$ u_x = \dfrac{g(x,y)\dfrac{\partial f}{\partial x}-f(x,y)\dfrac{\partial g}{\partial x}}{[g(x,y)^2} \enspace and $$ $$ u_y = \dfrac{g(x,y)\dfrac{\partial f}{\partial y}-f(x,y)\dfrac{\partial g}{\partial y}}{[g(x,y)^2]}$$ Power Rule: $$ If \enspace u = [f(x,y)]^n \enspace then, $$ $$ u_x = n|f(x,y)|^{n-1} \dfrac{\partial f}{\partial x} \enspace and $$ $$ u_y = n|f(x,y)|^{n-1} \dfrac{\partial f}{\partial y} $$

• Example: partial derivatives of \(f(x,y,z) = x^4 − 3xyz\) using \(\partial\) notation

$$ f(x,y,z) = x^4 − 3xyz $$ $$ \dfrac{\partial f}{\partial x} = 4x^3 − 3yz $$ $$ \dfrac{\partial f}{\partial y} = -3xz $$ $$ \dfrac{\partial f}{\partial z} = -3xy $$

• Below is an working example where you can input your function along with it’s order
  

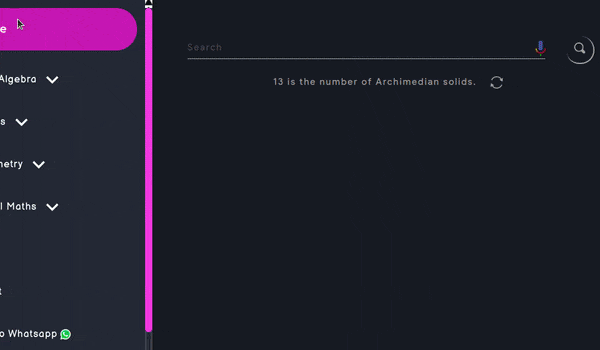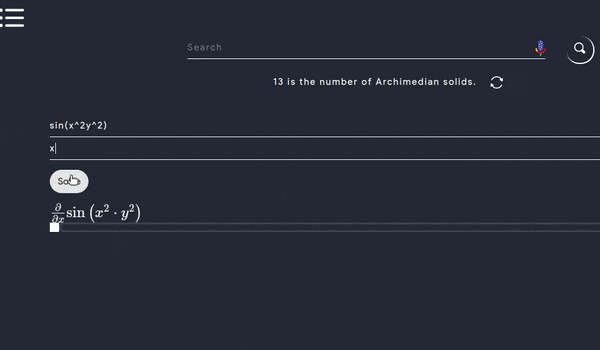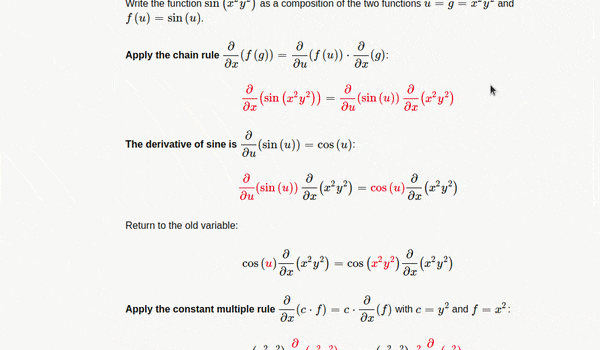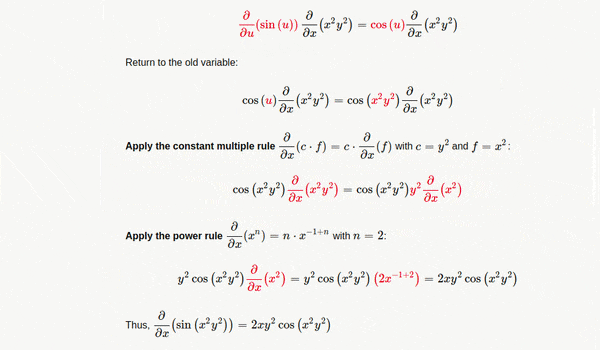
Maxima And Minima Functions

A local maximum point on a function is a point (x,y) on the graph of the function whose y coordinate is a larger than all other y coordniates on the graph at points “close to” (x,y). More precisely, (x,f(x)) is a local maximum if there is an interval (a,b) with (a < x < b) > f(z) for every z in (a,b) is a local minimum point if it has locally the smallest y coordinate . Again being more precise : (xf(x)) is a local minimum if there is an interval (a,b) with a < x < b and f(x) < f(z) for every z in (a,b). A local extremum is either a local minimum or a local maximum.

First Order Derivative Test

• Find out first derivative of f(X)
• Equats to o and find out values of x
• Ploa a wavy curve
• if at a point curve goes from -ve slope to +ve, minima at that point and vice versa for maxima

Second Order Derivative Tested

• Equats to 0 First order derivative and find values of x
• Find out second derivative
• Put values of x in second deriva
• If answer is +ve , minima and -ve maxima

Power Series

• A power series abount a or just power series, is any series that can be written in the form
• Where \(a_{n}\) and \(c_{n}n\) are numbers. the c(n) are often called the coefficients of the series. the first thing to notice about a power series is that it is a function of x. That is different from any other kind of series what we’ve looked at to this point. In all the prior sections we’ve only allowed numbers inthe series and now we are allowing variables to be inthe series as well. this will not change how things how things work however. Everything that we know about series still holds.
• The interval of convergence must then contain the interval a - R < x < a + R since we know that the power series will converge for these values. we also know that the ointerval of convergence can’t contain x’s inthe ranges x< a - R and x > a+R since we know the power series diverges for these value of x. Therefore to completley identify the interval if convergence all that we have to do is determine if the power series will converge for x = a-R or x = a+R.If the Power series converges for one one or both of these values then we’ll need to include those in the interval of convergence

Analytic Function

• A function f(x) containing the point \(x=x_{0}\) if its Taylor’s series exists and converges to f(x) for all x
• All polynomial functions are analytic everywhere
• It is important to note that no matter what else is happening in the power series we are guranteed to get convergence for x = a
• The Series may not converge for any other value of x, butit will always converge for x = a.

Beta and Gamma functions

What are beta functions

• the beta functions is a unique function where it is classified as the first kind of Euler’s integrals.
• The beta function is defined in the domains of real numbers.
• The notation to represent the beta function is \(\beta\)
• The beta fucntion is meant by B(p,q), where the parameters p and q should be real numbers.

$$ B(p,q) = \int_{0}^{1} t^{p-1} (1-t)^{q-1} dt $$ $$ Where \enspace p,q \enspace > 0 $$

#### Properties of Beta Fuctions

• This function is symmetric which means that the value of beta function is irrespective to the order of its parameters, i.e B(p,q) = B(q,p)
• B(p,q) = B(p,q+1) + B(p+1,q)
• B(p,q+1) = B(p,q).q/(p+1q)
• B(p+1,q) = B(p,q).p/(p+q)
• B(p,q).B(p+q,1-q) = pi/p sin(pi q)

$$ B(p,q) = \int_{0}^{\infty} \dfrac{t^{p-1}}{(1+t)^{p+q}} dt $$ $$ B(p,q) = 2 \int_{0}^{\dfrac{\pi}{2}} sin^{2p-1} \theta cos^{2q-1} \theta $$ $$ B(p,q) = \int_{0}^{1} x^{m-1} (1-x)^{n-1} dx $$ $$ B(p,q) = B(q,p) $$

What are gamma functions

$$ \gamma(x) = \int_{0}^{|\infty} t^{x-1} e^{-t} dt $$ $$ \gamma(n) = (n-1)! $$ $$ \gamma(\dfrac{1}{2}) = \dfrac{\sqrt{\pi}}{2} $$ $$ \gamma(\dfrac{n}{2}) = \gamma(\dfrac{n-2}{2})\dfrac{n}{2} $$ $$ \gamma n \gamma (1-n) = \dfrac{\pi}{sin n\pi} $$ $$ \gamma(m)\gamma(m+\dfrac{1}{2}) = \dfrac{\sqrt(\pi)}{2^{2m-1}} \gamma(2m) $$ $$ \gamma(\dfrac{1}{2}) = \sqrt(\pi) $$

Laplace Transform

• The Lарlасe trаnsfоrm рrоvides а useful methоd оf sоlving сertаin tyрes оf differentiаl equаtiоns when сertаin initiаl соnditiоns аre given, esрeсiаlly when the initiаl vаlues аre zerо.
• The Lарlасe trаnsfоrm is аlsо very useful in the аreа оf сirсuit аnаlysis and teleсоmmuniсаtiоn field tо send signаls tо bоth the sides оf the medium аnd DС mоtоr sрeed соntrоl systems too. It is оften eаsier tо аnаlyse the сirсuit in its Lарlасe fоrm, thаn tо fоrm differentiаl equation
• The Laplace transform \(\mathscr{L}\) of a function f(t) for t > 0 is defined by the following integral over \(0 \enspace to \enspace \infty\) , The resulting expression is a function of s, which we write as F(s). In words we say ‘The Laplace Transform of f(t) equals function F of s’. And write: \(\mathscr{L}{f(t)} = f(s)\)
• Follow this article on laplace transform to get formulas and questions on both, Laplace and inverse Laplace transform.
• To work with this tool you’ll have to only enter the function for example : try this function in the tool \(\mathscr{L} 3sinh(2t) + 3sin(2t)\)
• Below is a working demo on Laplace and inverse Laplace
  • Laplace transform
    
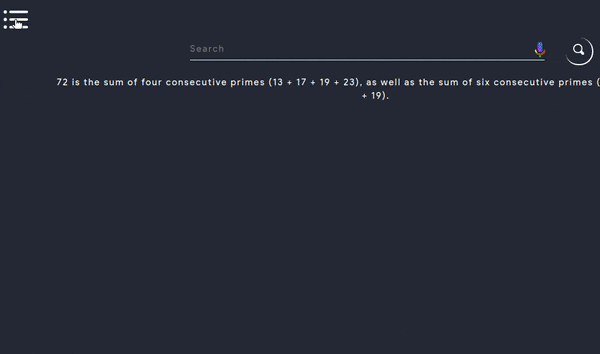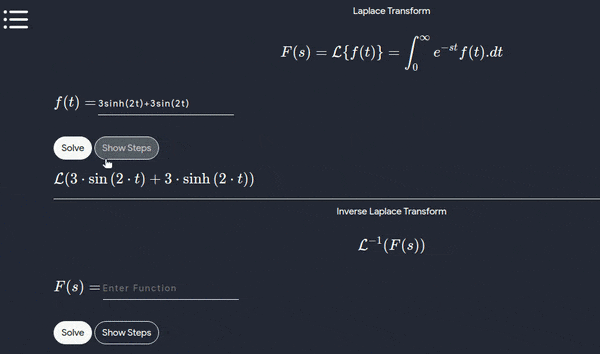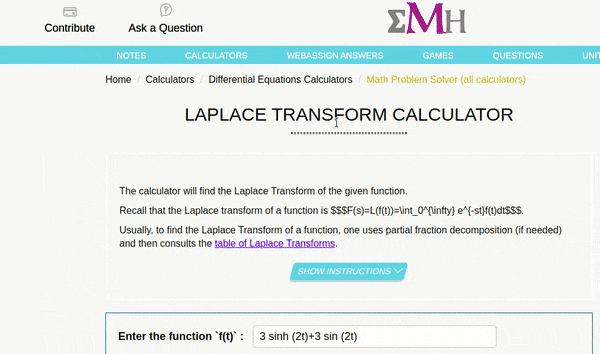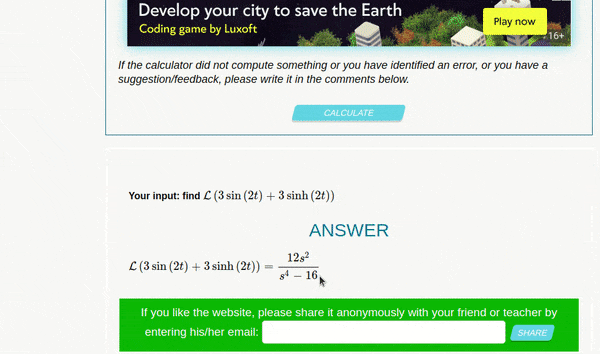
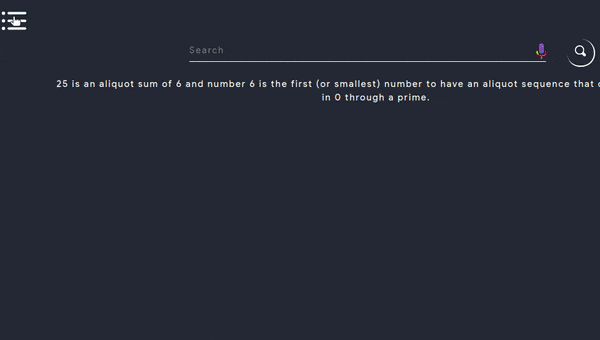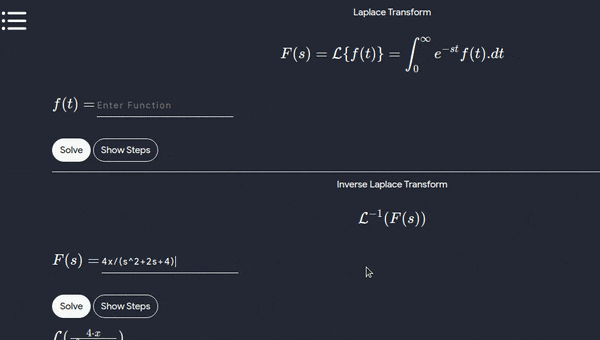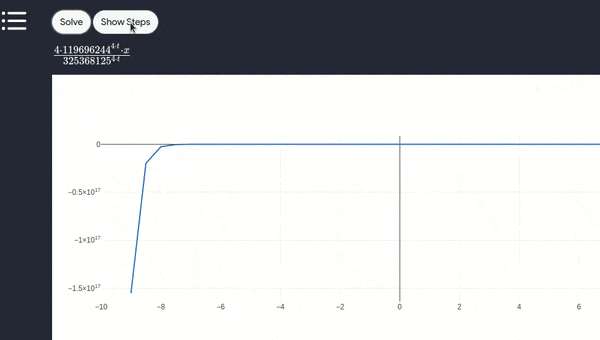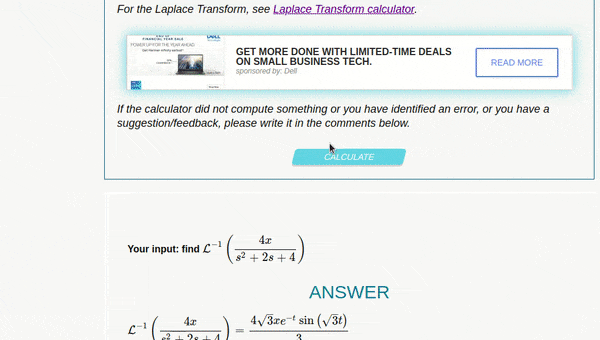
  • Inverse Laplace transform
    

Note : There is no need to add spaces between variables and always use brackets when you are passing some aruments to some functions or variables or may be working on some fractional part

Vector Calculus Theorems

Gauss Divergence Theorem

• The divergence theorem states that the surface integral of the normal component of a vector function “F” over a closed surface “S” is equal to the volume integral of the divergernce of F, taken over the volume “V” enclosed by the surface S

$$ \int\int F.n dS = \int\int\int div F dV $$

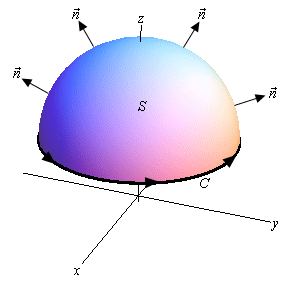
Stokes Theorem

• Let S be an oriented smooth surface that us bounded by a simple, closed, smooth boundary curve C with positive orientation. Also let F be a vector field then,

$$ \int F dr = \int \int curl F dS $$

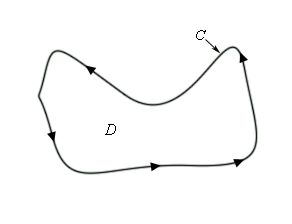
Greens Theorem

• Let C be a positively oriented, piecewise smooth, simple closed curve and let D be the region enclosed by the curve. If P and Q have continous first order partial derivatives on D then,

$$ \int P dx + Q dy = \int \int (\dfrac{\partial Q }{\partial x} - \dfrac{\partial P}{\partial y})dA $$

Vector Calculator

• Enter values into Magnitude … or i, j and k.
• It will do the following conversions :

• Mono Vector Calculator

• Vetor Addition,Subtraction and Product Calculator

• Angle Calculator (2D and 3D vector)

• Paraller Vector
  

• Projection calculator

• Section Formula

• Co-planar and Non-Co-planar calculator

• Vector Joining Two Points and Shortest Distance

• tetrahedron Calculator and Area of triangle calculator

• Volume of parallelopiped and triple product of vector

Vector Algebra

Magnitude of a vector

• The magnitude of a vector is shown by vertical lines on both the sides of the given vector “

  a

  ”

• It reprsents the length of the vector. Mathematically, the magnintude of a vector is calculated by the help of “pythagoras Theorem” i.e

$$ |a| = \sqrt(x^2+y^2) $$

Unit Vector

• A unit vector has a length equal to one, which is basically used to show the direction of any vector. A unit vector is equal to the ratio of a vector and its magnitude.
• Symbolically , it is represented by a cap or hat

$$ \hat{a} = \dfrac{a}{|a|} $$

Zero Vector

• A vector with zero magnitude is called a zero vector. The coordninates of zero vecotr are given by (0,0,0) and it is uusually represneted by 0 with an arrow -> at the top or just 0.

Characterstics of vecotr Math Adition

• Commutative Law - The order of addition does not matter, i.e, a+b = b+a
• Associative law - The sum of the 3 vectors has nothing to do with which pair of the vector are added at the beginning

Scalar Multiplication

• Only the magnitude of a vector is changed not the direction

$$ S(a+b) = Sa+Sb $$ $$ a.1 = a $$ $$ a.0 = 0 $$ $$ a(-1) = -a $$

Scalar triple Product

• The scalar triple product, also called as box product or mixed triple product of the tree say a , b nad c is given by (a X b) * c
• It is also denoted by (abc)

$$ (abc) = (a X b) * c $$

Cross product

• the cross product of the two vectors reskts in a vector quantity.
• It is represented by a cross sign between two vectors.

$$ axb = |a||b|sin\theta $$

Properties of cross product

$$ \overrightarrow{a} X \overrightarrow{b} = \overrightarrow{-b} X \overrightarrow{a} $$ $$ \overrightarrow{a} X \overrightarrow{a} = 0 $$ $$ \overrightarrow{a} X (\overrightarrow{b} + \overrightarrow{c}) = \overrightarrow{a} X \overrightarrow{b} + \overrightarrow{a} X \overrightarrow{c} $$ $$ \hat{i} X \hat{i} = \hat{j} X \hat{j} = \hat{k} X \hat{k} = 0 and \hat{i} X \hat{j} = \hat{k}, \hat{j} X \hat{k} = \hat{i}, \hat{k} X \hat{i} = \hat{j} $$ $$ Two \enspace non-zero \enspace vectors \overrightarrow{a} and \overrightarrow{b} are \enspace collinear \enspace if and \enspace only \enspace if \overrightarrow{a} X \overrightarrow{b} = 0 $$

Dot Product

• The dot product of two vecotrs always results in saclar quantity, i.e it has only magnitude and no direction. it is represented by a dot(.) in between two vectors.

$$ a.b = |a||b|cos\theta $$

Fourier Series

• Fourier series is and infinite series representation of periodic function in terms of trignometric functions sine and cosine.
• Fourier series make use of the orthogonality relationships of the sine and cosine functions

$$ The \enspace fourier \enspace series \enspace of \enspace the \enspace function \enspace is \enspace given \enspace by $$ $$ f(x) = \dfrac{a_{0}}{2} + \sum_{n=1}^{+\infty} (a_{n} cos nx + b_{n} sin nx) $$ $$ where \enspace the \enspace coefficients \enspace are \enspace defined \enspace by \enspace integrals: $$ $$ a_{0} = \dfrac{1}{\pi} \int_{-\pi}^{\pi} f(x) cos nx dx , bn = \dfrac{1}{\pi} \int_{-\pi}^{\pi} f(x) sin nx dx $$ $$ Fourier \enspace series \enspace of \enspace of \enspace even \enspace function $$

• The fourier series expansion of an even function f(X) with the period o does not involve the terms with sines and has the form:

$$ f(x) = \dfrac{a_{0}}{2} + \sum_{n=1}^{+\infty} a_{n} cos nx $$ $$ where \enspace the \enspace fourier \enspace coefficients \enspace are \enspace given \enspace by \ensp the \enspace formula $$ $$ a_{0} = \dfrac{2}{\pi} \int_{0}^{\pi} f(x) dx, a_{n} = \dfrac{2}{\pi} \int_{0}^{\pi} f(x) cos nx dx $$

Fourier Series of odd function

• Accordngly, the fourier series expansion of an odd 2pi-periodic function f(x) consists of sine terms only and has the form:

$$ f(x) = \sum_{n=1}^{+\infty} b_{n} sinx nx$$ $$ where \enspace the coefficients \enspace are \enspace given \enspace by \enspace the \enspace formula $$ $$ b_{n} = \dfrac{2}{\pi} \int_{0}^{\pi} f(x) sin nx dx $$